Hvis du skal beregne en enkelt korrelationskvotient, vil du opdage at Excels dataanalyseværktøj Korrelation gør det samme som regnearksfunktionen KORRELATION, selvom outputtet er i tabelform. Dette værktøj bliver nyttigt når du skal beregne flere korrelationer på et datasæt.
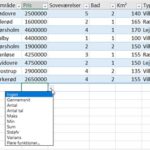
Figuren viser fire aktiekurser over et år på ugebasis sammen med dialogboksen for dataanalyseværktøjet Korrelation.
Følg disse trin for at bruge dette værktøj:
1. Indtast data i regnearket og inkluder overskrifter for kolonnerne.
I dette eksempel er dataene (inklusiv overskrifter) i B1:E53.
2. Vælg fanen Data -> Analyse -> Dataanalyse for at åbne dialogboksen Dataanalyse.
3. I dialogboksen Dataanalyse rulles ned i listen Analyseværktøjer og vælg Korrelation.
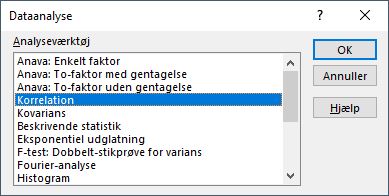
4. Klik OK for at åbne dialogboksen.
Denne dialogboks er vist i figuren nedenfor.
5. I feltet Inputområde indtastes celleområdet, der indeholder alle data.
Jeg har indtastet $B$1:$E$53. Bemærk $ tegnet for absolutreference. Excel tilføjer dem når du markerer celleområdet i regnearket.

6. Til højre for Outputindstillinger vælges en radioknap for at indikere, om dataene er organiseret i kolonner eller rækker.
Jeg har valgt radioknappen Kolonner.
7. Hvis celleområdet inkluderer kolonneoverskrifter, vælges checkboksen Etiketter i første række.
Jeg har inkluderet overskrifter i området, så jeg har valgt denne boks.
8. I Outputindstillinger vælges en radioknap for at indikere, hvor du vil have resultatet.
Jeg har valgt Ny regnearksfane for at placere resultatet på en ny fane i projektmappen.
9. Klik OK.
Fordi jeg har valgt Ny regnearksfane bliver et nyt regneark åbnet med resultatet.
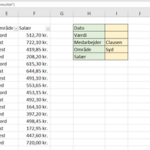
Tabel output
Figuren viser værktøjets tabeloutput, efter jeg har udvidet kolonnerne. Tabellen er en korrelationsmatrix.

Hver celle i matricen repræsenterer variablen i rækken med variablen i kolonne. For eksempel viser cellen B3 korrelationen af AIRBUS med SAS. Hver celle i hoveddiagonalen indeholder 1. det er fordi hver hoved diagonalcelle repræsenterer korrelationen af en variabel med den selv.
Det er kun nødvendigt at udfylde halvdelen af matricen. Cellerne oven for hoveddiagonalen ville indeholde de samme værdier som cellerne under hoveddiagonalen.
Hvad er korrelationskoefficienten?
Korrelationskoefficienten er et statistisk mål, der beregner styrken i forholdet mellem de relative bevægelser af to variabler. Værdierne varierer mellem -1,0 og 1,0. Et beregnet tal større end 1,0 eller mindre end -1,0 betyder, at der er en fejl i korrelationsmåling. En korrelation på -1,0 viser en perfekt negativ korrelation, mens en korrelation på 1,0 viser en perfekt positiv korrelation. En korrelation på 0,0 viser intet forhold mellem bevægelsen af de to variabler.
Korrelationsstatistikker kan bruges i finans og investerings branchen. For eksempel kunne en korrelationskoefficient beregnes for at bestemme korrelationsniveauet mellem prisen på råolie og aktiekursen for et olieproducerende selskab. Da olieselskaber har en større fortjeneste, når oliepriserne stiger, er sammenhængen mellem de to variabler meget positiv.
Forstå korrelationskoefficienten
Der er flere typer korrelationskoefficienter, men den, der er mest almindelig, er Pearson-korrelation (r). Denne måler styrken og retningen for det lineære forhold mellem to variabler. Den kan ikke fange ikke-lineære forhold mellem to variabler og kan ikke skelne mellem afhængige og uafhængige variabler.
En værdi på nøjagtigt 1,0 betyder, at der er et perfekt positivt forhold mellem de to variabler. For en positiv stigning i en variabel er der også en positiv stigning i den anden variabel. En værdi på -1,0 betyder, at der er et perfekt negativt forhold mellem de to variabler. Dette viser, at variablerne bevæger sig i modsatte retninger – for en positiv stigning i en variabel er der et fald i den anden variabel. Hvis korrelationen mellem to variabler er 0, er der ingen sammenhæng mellem dem.
Forholdets styrke varierer i grader baseret på værdien af korrelationskoefficienten. For eksempel viser en værdi på 0,2, at der er en positiv sammenhæng mellem to variabler, men den er svag og sandsynligvis ubetydelig. Eksperter anser ikke korrelationer for at være betydningsfulde, før værdien overstiger mindst 0,8. Imidlertid ville en korrelationskoefficient med en absolut værdi på 0,9 eller større repræsentere et meget stærkt forhold.